Stanford CS229 강의 요약 Machine Learning - Course Introduce | Lecture 1 - Andrew Ng (Autumn 2018)
한 2,3주 전에 영상을 보고 현생사느라 바빠서 정리를 못했다. 이번 강의는 Anand Avati 인도 교수님께서 해주셨다. 원래도 통계학을 하시는걸로 알고 있으며, Machine Learning에서 NGBoost 모델을 만드신 교수님으로 알고있다. 수학적인 내용이 많으며, 따라가기 어려웠다는 댓글도 많으며, 나도 기억이 잘 안나지만, 아무튼 정리해보자
이번 강의 목표
1. Perceptron Algorithm
2. Exponential Family
3. Generalized Linear Model
4. Softmax Regression. (Multi class Regression)
Recap 및 Perceptron Algorithm
- 지난주에 배운 Logistic Regression을 간략화 하면 왼쪽 아래와 같다. 그래프의 모양 및 Logistic Regression에 대한 수식 g(z)로 표기되어 있으며, 이는 Sigmoid의 수식과 같다. 우리가 만들기 원하는 Regression Model의 경우, 모델 파라미터 θ와 입력 x에 의해 y값이 결정되므로 z를 θT⋅x로 치환하여 Logistic Regression Model의 수식은 hθ(x)가 된다.
- 그렇다면 Perceptron Algorithm은 어떻게 생겼을까? 가운데 임의의 지점 z를 바탕으로 z보다 크거나 같은 경우 1, z보다 작을 경우 0을 만드는 함수 g(z)가 Perceptron Algorithm이다. Logistic Regrssion과 동일하게, z를 θT⋅x로 치환할 경우, hθ(x)를 정의할 수 있다.
- 따라서 θj := θj + α(y(i) - hθ(x(i))⋅xj(i)) 와 같이 업데이트 하는 방식이 동일하다는 것을 알 수 있다. 그리고 이 업데이트 하는 방식은 SGD와 동일하다는 것을 알 수 있다.

- 우리가 동그라미와 네모 클래스를 분류하는 모델을 찾는다고 할 때, 왼쪽의 점선과 같이 모델이 기본적인 Linear형태의 그래프를 가진다면, 새로 들어온 입력 네모는 동그라미로 잘못 예측 될 것이다.
- 이 때 잘못된 예측 네모에 대해 얼마나 잘못된 예측을 했는지에 대한 주황색 선 (x, θ)를 그리고, 새로운 θ'을 구한 후, 이와 직각인 x'를 구해서 x가 x'에 대해 움직인 만큼 θT⋅x를 θ'T⋅x'인 자홍색 선을 그리는 방식으로 우리의 모델이 Update를 하게 된다.

Exponential Family
- Regression Model의 분포- y|x; θ ~ 𝒩(μ, σ**2), Classification Model의 분포 - y|x; θ ~ Bernoulli(ϕ) 를 가진다고 하자.
이 때 μ와 ϕ는 x와 θ에 대해 근사하는 정의이다.
- 여기서 위의 Regression Model과 Classification Model 둘 다 Generalized Linear Model에 속한다는 것을 보여줄 것이다.
- 위의 과정을 보여주기 전에 Exponential Family Distribution에 대해 배우고 가자.

- 위의 수식은 다양한 분포의 종류가 위의 수식에 해당될 때, Exponential Family로 불린다는 것이다.
- 수식으로만 파악하기엔 한계가 있어서 추가적인 설명을 하며 위의 수식을 설명해보겠다.
- 위와 같은 분포를 가지는 Gaussian 분포도 Exponential family에 속한다. 자세한 내용은 밑에서 다루는데, 가볍게 설명하자면, 우리가 알기 원하는 데이터의 분포 y는 자연 파라미터 η가 주어졌을 때의 분포이다.
- 즉 η는 PDF (Probability Density function)를 만들어내는 여러개의 파라미터이며, 이 η가 Canonical parameter라고도 불리기도 한다.
- Canonical parameter는 PDF에서의 평균을 의미한다. 이 자연파라미터와 Canonical parameter가 interchangeable하게 쓸 수 이유는, 위에서 Gaussian분포를 Exponential family 수식의 형태로 바꿨을 때 둘이 같기 때문이다.
구체적으로 설명하자면,
- p(y; η)는 우리가 관측하고 싶은 데이터 y의 분포로, 자연 파라미터 η를 사용하여 데이터 y에 대한 분포를 알아낼 것이다.
- y는 데이터
- η는 Natural Parameter (Canonical parameter)는 자연 파라미터로, Anand교수님의 말과 내가 찾아본 바에 의하면를 섞으면 "capture the properties and encapsulate the relationship which distribution of the data x."로, 특징을 찾고, 데이터 x에 대한 분포관계를 요약한다고 할 수 있다. 여기서 입력 데이터는 y가 될 것이다. θ와 비슷한 역할이라고 보면 편하다.
- T(y)는 Sufficient statistic으로 우리는 주로 T(y) = y인 상황만 고려한다.
a(η)는 log partition function → exp와 합쳐진 exp(-a(η))은 Distribution p(y;η)의 합 또는 적분 한 y값이 1이 되게 하는 Normalization constant이다.
- 우리가 하고자 하는 것은, 고정된 T, a, b를 가지고 η를 변화시킬 때 마다 새로운 분포를 얻는다는 것인데, 이 분포들은 전부 Exponential Family에 속한다는 것이다. 따라서 우리가 지금까지 본 Bernoulli, Gaussian 등 과 같은 분포를 여기에 집어 넣은 후 실제로 저 분포가 나오는지 볼 것이다.
Exponential Family - Bernoulli편
- Bernoulli 분포는 평균이 ϕ일 때, Bernoulli(ϕ)로 정의할 수 있다. 분포는 아래 그림과 같다.
- 이 Bernoulli 분포는 𝒴 ϵ {0, 1} 이므로 p(𝒴 = 1|ϕ) = ϕ or p(𝒴 = 0|ϕ) = 1 - ϕ로 나타낼 수 있다.

- 이 Bernoulli 분포를 수식으로 나타내면 ϕy⋅(1-ϕ)^{1-y}가 될 것이며, 이를 차례로 풀어내면 제일 마지막 수식과 같다.
- 이는 우리가 위에서 보여주었던 Exponential Family의 분포와 같다.

- 재미있는 점은 우리의 자연 파라미터 η를 ϕ에 대해 역으로 변환시키면 ϕ = 1/(1+e^{-η})로 sigmoid function와 비슷한 함수가 나오게 된다는 것이다. 그리고 Exponential Family를 정의하면서 얻은 값들은 아래와 같다.
- 또한 여기서의 Canonical Parameter는 Bernoulli 분포의 평균을 나타내는 ϕ를 의미한다. 그리고 η와 ϕ의 대한 관계는 위와 같이 ϕ = 1/(1+e^{-η})로 η = log(ϕ/(1- ϕ))로 정의할 수 있다. 여기서의 자연 파라미터와 Canonical parameter는 같지 않지만, 1대1로 대응된다는 것을 알 수 있다.
- 이러한 점에서 Canonical Parameter는 Canonical Link function이라고도 불린다.

Exponential Family - Gaussian편
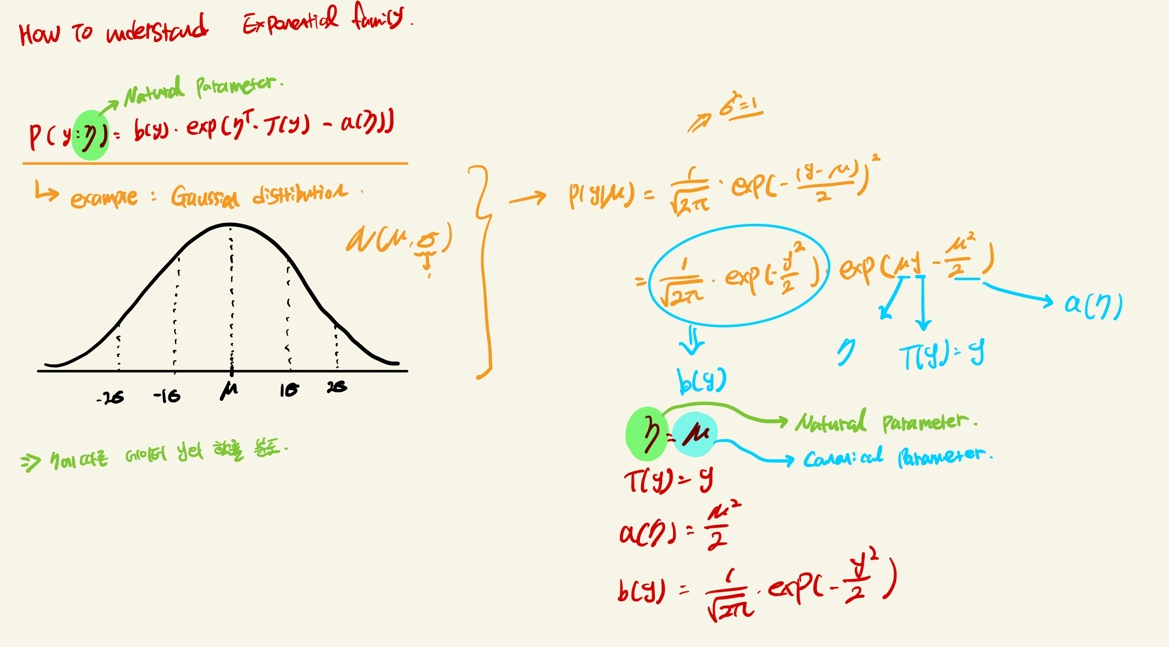
- Gaussian의 경우 σ**2가 θ 혹은 hθ(x)를 고르는데 영향이 주지 않기 때문에, 우리의 표준편차는 σ**2=1로 가정하고 간다.
- 왼쪽 아래는 Gaussian 분포의 사진이다. 빨간색 그래프가 평균 0, 표준편차 1의 Standard normal distribution이다.
- Gaussian distribution의 수식은 너무 유명하니 외우면 좋을 것 같다. 아래의 p(y; u)에서 y-μ의 분모로 σ가 들어가면 Gaussian distribution의 분포 수식과 똑같아진다. 여기서는 σ**2=1로 가정했기에 사라졌다.



- 따라서 Exponential family에 속하는 Gaussian 분포 또한 위에서 정의한 파라미터들로 바뀔 수 있다. (상단 우측)
- 그 외에도 Multinomial, Poisson 등이 있는데, Poisson이 Exponential Family에 속하는지를 증명하는 것은 숙제라고 한다.
Question.
질문중에 아주 좋은 질문이 있었는데, 왜 Exponential Family를 사용해야 하는지가 질문이다. 나도 강의를 들으면서 왜 Exponential Family로 연결이 되어야만 하는가에 대한 고민을 했었는데,
1. 아주 좋은 수학적 특징을 가지고 있기 때문이며
2. 이는, 만약 우리가 Exponential Family 분포에 대해 Maximam likelihood를 Neural network로 수행할 때, optimize problem을 concave하게 풀 수 있다는 점으로 이어지기 때문이다.
3. Generalized Linear Model
4. Softmax Regression. (Multi class Regression)
위의 2개는 다음 포스팅에서 하도록 하겠다.



