이전 강의 요약
Stanford CS229 강의 요약 Machine Learning Course, Lecture 1 - Andrew Ng (Autumn 2018)
Week 3 Topic
1. Linear Regression (Recap)
2. Locally weighted Regression
3. Probabilistic interpretation
+ Why the cost function is MSE?
- 위와 관련된 내용은 여기서 볼 수 있다.
Stanford CS229 강의 요약 Machine Learning - Locally Weighted & Logistic Regression | Stanford CS229: Machine Learning - Lect
Week 3 Topic & Week 2 Recap 1. Linear Regression (Recap) 2. Locally weighted Regression 3. Probabilistic interpretation + Why the cost function is MSE? 4. logistic regression (3-2 다음 포스팅에서) 5. Newton's method (in losgistic regression) (3-2
187cm.tistory.com
4. logistic regression
5. Newton's method (in losgistic regression)
4. logistic regression
- 우리가 예측해야하는 y ∈ {0, 1} 일 때, 간단하게 0부터 1사이 값을 만족시키는 아래와 같은 함수를 정의 가능하다. Sigmoid와 같으며 logistic function이라 불린다.
- 그림으로 시각화하면 우측아래와 같다. +∞로 갈 경우 1, -∞로 갈경우 0이다.
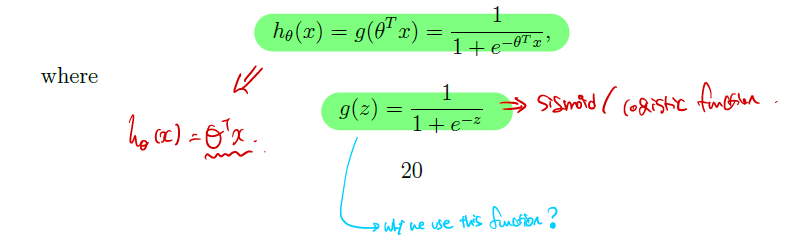
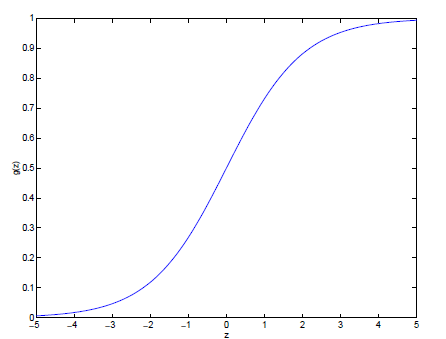

- 이 Sigmoid function을 미분하는 경우는 다음과 같다. 조금더 자세한 내용은 여기에 담아뒀다.
Sigmoid 미분하기
우선 시그모이드는 다음과 같이 정의된다. $$ \sigma(x) = \frac{1}{1+e^{-x}} $$ 따라서 도함수를 이요한 몫의 미분법을 이용해 아래와 같은 수식이 유도된다는 것을 먼저 인지하자. $$ \frac{1}{g(x)'} = \lim\li
187cm.tistory.com
- 이제 y=1일때 (malignant O), y=0일 때 (malignant X)로 정의하여 사용할 수 있다.
- 영상에서 들어온 질문으론 y=1일 때 1- hθ(x), y=0일 때 hθ(x)를 바꿀 수 있는지 물어봤는데, 가능은하나 관습이라 바꾸지 말라고 하셨다.
- 그리고 이 둘의 수식을 하나로 합쳐서 p(y|x;θ) = hθ(x)^y⋅(1-hθ(x))^(1-y)로 만들 수 있다. y=0, 1을 각각 넣어보면 된다.

- 그리고 이 p(y|x;θ)를 가지고 우리는 Maximum likelihood L(θ)를 구할 수 있다.


How to maximize the likelihood in the Logistic Regression.
- 우선 미분 과정은 간단히 설명하면 다음과 같다.
1. chain rule에 의해 뒷부분 ∂/∂θ⋅g(θT⋅x)이 생기며, 앞부분은 hθ'(x) = g'(x) = ()안의 결과
2. ∂/∂θ⋅g(θT⋅x)을 미분합니다.
3. 수식 전개
4. 최종 수식 (y-hθ(x))⋅xj
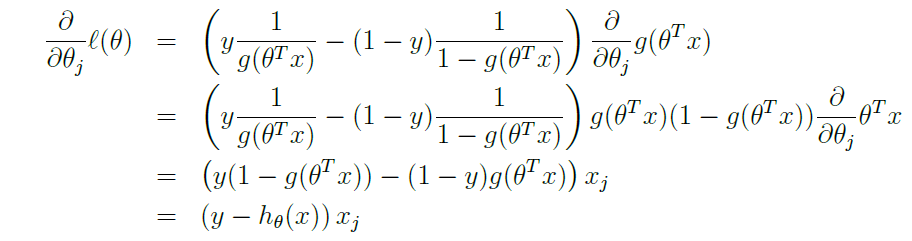
- 또한 logistic과 Linear의 GD algorithm은 반대인데, 그 이유를 잠깐 풀어보고자 한다.
- logistic regression에서의 gradient descent algorithm을 사용한다. θ := θ + α∇θ(ℓ(θ))
- Linear regression에서의 gradient descent algorithm은 θ := θ - α∇θ(J(θ))
- 차이점이 있다면 log likelihood + MSE (Minimize) 와 log likelihood (Maximize)사용의 차이, Linear Regression에서도 Maximize를 했다고 볼 순 있으나, J(θ)를 0으로 수렴시키기 위해 hθ(x) - y를 0으로 minimize시키려 했다.
- Logistic은 바로 업데이트를 시도한다고 보면 될 것 같다.
- 그리고 둘의 차이를 보면 - α∇θ(y(i) - hθ(x(i))) 와 +- α∇θ(hθ(x(i)-y(i)))는 진짜 -를 곱해주면 된다. 부호 바꾸면 똑같다.
- 따라서 그림으로 보면 파란색과 빨간색이 결국엔 굉장히 유사한 작업을 한다는 것을 앐 수 있다.
- Logistic Regression 또한 Local minima는 없다. 하지만 데이터의 분포를 가지고 normal equation을 통해 정답을 알 수 있는 y=ax+b형태의 linear Regression과 달리 Rogistic Regression은 반복을 통한 알고리즘이므로 normal equation을 사용할 수 없다.



Newton's Method in Logistic Regression
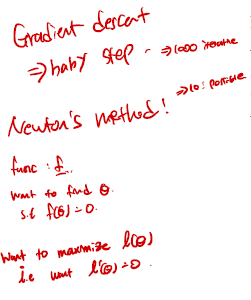

- 수렴이 매우 빠르다! 하지만 Cost가 매우 높다.
- 2번 미분한다고 생각하면 편하다.

- 1차 미분 선을 그린 후, 1차 미분선을 연장하여 1차 미분선이 0이되는 지점에서 다음 반복을 실시한다.
- 수식으로 나타내면 아래와 같다. 그리고 이 f(θ) = f(θt) = ℓ'(θt) 가 되므로 2차 미분이 되게된다.

Hessian
- 위와 같이 2차 미분을 한 행렬을 우리는 Hessian이라고 부르고 H로 사용하기로 합니다.
- 근데 일반적인 1차 미분보다 값이 비싸다.






