강의 요약
1. Normal eqation
2. Linear Regression
3. LMS Algorithm
4.왜 X는 invertible 해야할까? (feat 다중공산성)
Chapter 1. Linear Regression.

- 이번엔 bedrooms라는 정보가 포함이 되었다. multi feature가 되었다. 따라서 x는 ℝ이 아닌 ℝ^2 가 된다. (LaTex화난다)
- 따라서 수식은 아래와 같이 x2에 대한 항이 하나가 추가가 되었다. x1은 Living area, x2는 bedrooms가 된다.
- 위에서 언급한 n이 이제는 2인 case를 처리해보자.
- θ는 parameter 혹은 weight라고 불린다.


- x0을 dummy feature로 적용을 하면 다음과 같이 간략하게 사용이 가능하다. h(x) = θ^T ⋅ x. 앞으로 자주 볼테니 기억하자
- 이제 이 h(x)를 잘 만들기 위해서 어떻게 해야할까, h(x)가 y와 가까워 지는게 목표이므로, J(θ)를 아래와 같이 정의한다.
- J(θ)를 우리는 Cost function이라고 부른다. 그리고 이 J(θ)를 최대한 작아지게 만드는 것이 목표이다.

- 음수를 피하기 위해 절대값, 제곱하고 루트 씌우기 등 다양한 방법이 있는데 왜 제곱을 했을까? 그건 Gaussian과 관련이 있다. 이 내용은 Week3에 나온다. 빼고 제곱하는 과정을 거친다. 1/2는 그냥 편의성이다.
1.1 LMS Algorithm (Least mean squares = Widrow-Hoff rule)
- 위에서 언급한대로 J(θ)를 Minimize하는 것이 목표이다. 그렇다면 어떻게 이 J(θ)를 최소화할까?
- Gradient descent Algorithm을 사용하여 최소화 하자.! (j = 0, ... d, θ는 전부 동시에 업데이트 된다.)
- := 는 할당한다는 뜻이다.
- α는 learning rate이다. 보통 0.01을 쓴다
- ∂은 미분기호이다. 특정 함수 J(θ)가 있을 때, 이 J(θ)의 기울기만큼 이동한다.
- 추가적으로 hθ(x) = h(x)와 같다고 본다. hθ(x)는 x그리고 θ를 모두 고려하는 샘플이 될 것이다.
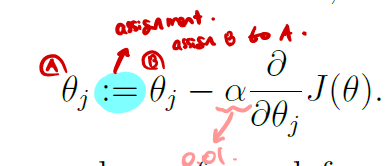

이제 이 J(θ)를 θj에 대해 미분하는 과정을 상세하게 유도하면 다음과 같다.
- 2번째 줄의 수식은 chain rule에 의해 ∂/∂θ ⋅ (hθ(x) - y) 가 반복된다. 그 이유는 2시 방향에 써뒀는데 잘 안보인다.
- 3번째 줄 수식은 2번째 chain rule 미분 사진을 참조하면, (hθ(x) - y)가 미분이 되어야한다. 그 전에 hθ(x)를 먼저 치환한다.
- 그러고 나서 θixi - y를 θj에 대해 미분하면, i=j일 때 빼고는 다 0으로 편미분 될 예정이니까 최종 수식 완성이다.
- 아래 아래의 오른쪽 수식 참고.

- θj := θj + α⋅(y(i) - hθ(x(i))⋅xj(i) 수식을 해석해보자면, θj에 대해 업데이트 할 때 y와 h(x)의 오차 뿐 아니라 해당 특징을 가지는 xj(i)까지 반영을 하겠다고 해석할 수 있다.
- 그래서 아까 gradient descent algorithm에 위에서 구한 ∂/∂θ ⋅ J(θ) 를 넣으면 위의 수식과 같다.
- 하지만 위의 그림의 첫 줄을 보면, 하나의 샘플에 대해 구한 것 이므로 m개의 샘플만큼 반복해야한다. (왼쪽)


- Linear Regression에서 J(θ)는 둥근 볼과 같은 2차함수 형태의 그래프를 만든다. 즉 Local minima가 존재하지 않다.
즉, Local-minima = Global-minima이다. 이 global minima란 우리가 찾아야 하는 최종적인 목표이다. local minima는 local적인 minima 즉, 그냥 작은 지점 중 일부이다. (나중에 더 쉽게 알려주겠다.)
- 위의 J(θ)가 왜 2차함수인지 이해가 안간다면 위의 hθ(x) = θ^T ⋅ x 를 다시 보고오자. x는 1차함수이며 Loss/cost function은 2차함수이다.
- 따라서 위와 같은 과정을 반복하게 된다면, θ= "→_0" 에서 ("→_0" = 모든 vector는 0 임을 나타냄.) 파란선으로 움직일 것


- 샘플마다 반복을 통해 θ를 업데이트 한다면, 혹은 모든 샘플을 계산 후에 θ를 업데이트를 한다면? 어떤 일이 벌어질까.
- 첫번째는 수렴을 하기가 굉장히 힘들 것이며, 수렴을 하더라도 그 다음 샘플의 오차가 크다면 최소화 지점을 벗어나 버릴 것이다. 반대로 모든 샘플을 계산 후에 θ를 업데이트하면, 너무 비용이 오래 걸려서 업데이트 하는데 오래걸릴 것이다.
- 그래서 Stochastic(확률적으로) 업데이트를 하자. 수렴은 아래와 같이 할 것.

1.2 The normal equations


- 이제 J(θ)를 0에 수렴시키기 위해 조금 더 구체적이게 정의를 한다.
- 오른쪽은 ∇θJ(θ) 는 "→_0"으로 셋팅된다는 것인데, θ가 0이 되는 것이 아닌, J(θ)를 미분한 것이 0이 되게 함으로써 최적의 수렴하는 점을 찾는다는 의미이다. 위에 보면 "→_0"가 뭔지 설명해두었다.
- 그리고 Andrew Ag 선생님께서 시간나면 풀어보라고 하신 Trace의 특성이다. Trace는 대각선의 합이다.

1.2.2 Least squares revisited
- x(1)T, x(2)T는 각각 n개의 feature들을 가지고 있으므로, 다음과 같이 row base matrix로 만들 수 있다.
(엑셀 한 줄 단위라 생각하면 편하다)
- Xθ와 θ의 선형 결합(Linear combination)을 통해 아래(왼쪽)와 같이 만들 수 있으며 이는 hθ(x(i)))로 바꿀 수 있다.
- 따라서 이를 이용해 Xθ - y = [ hθ(x(i)) - y(i) ] 수식이 됨을 보일 수 있다.


- 그리고 이 수식을 통해 아래와 같이 원래 J(θ)를 유도할 수 있다. Transpose 및 원형의 dot product가 우측과 같이 전개될 수 있는 이유는 아래의 오른쪽 그림을 참고하면 된다.
- 이 수식의 유도과정이 이해가 되지 않는다면 아래서부터 위로 올라가며, 반대로 유도를 하는 것이 이해가 빠를 것이다.


Normal equations.
- 그리고 아래 부분은 통째로 들고왔는데 차근차근 풀어보면 다음과 같다.
1. ∇θJ(θ) ≈ 0 이 되도록 하는 것이 우리의 목표이다. why: ∇θJ(θ) ≈ 0 이면 수렴을 통해 움직이지 않아도 된다는 뜻이다
2. 위에서 J(θ)가 1/2 ⋅ (Xθ - y)^T ⋅ (Xθ - y) 임을 보였기 때문에 이것을 대입하여, 이 식을 θ에 대해 미분한다.
2-2. 수식을 전개하면 다음과 같다.
- yT⋅y는 y(1)^2, y(2)^2, ... y(m)^2 과 같은 형태를 띄게 것이다. 이는 θ와 상관이 없으므로 미분을 통해 0이된다.
- (Xθ)T⋅y 는 aT⋅b = bT⋅a 를 통해 (Xθ)T⋅y = yT(Xθ) 형태로 바꿔준다
3. yT(Xθ)를 합쳐준다
4. 4번은 아래의 설명을 보면 친절하게 나와있다. 혹은 왼쪽 중간 가운데 수식을 보자.
- 그래도 정리를 하면 ∇x ( xT⋅A⋅x) = 2Ax 이므로, θT⋅(xT⋅x)⋅θ = 2⋅xT⋅x⋅θ이 된다.
5. ∇x ( bT⋅x) = b이므로, -2 (xT⋅y)T⋅θ = -2θ⋅xT⋅y 이다.
6. 0 = ∇θJ(θ) = xT⋅x⋅θ - xT⋅y 이므로, 이 수식은 xT⋅x⋅θ = xT⋅y가 된다.
+ 그리고 이 수식을 θ를 기준으로 정리하면 제일 아래와 같은 식이 나오게 된다.

그리고 강의를 마치며 Andrew Ng선생님께서는 이 X가 non-invertible할 경우엔 어떻게 될까요? 라는 질문을 하는데, non-invertible이란, 역행렬이 가능한지를 묻는 것이다. 역행렬이 불가능하다는 말은 중복되는 feature가 존재하거나, row가 중복되거나, 다중공산성과 같은 문제가 일어나 redundant feature, linearly dependent한다는 문제가 생긴다고 말한다.
- 다중공산성: feature들 간의 상관관계가 높아서 특정 feature가 영향을 더 많이 주게 되는 현상.
ex) Boston 집 값 예측에서 부지의 면적, 1층의 면적, Bedrooms, 차고의 여부 등 과 같은 특징이 있을 때, 부지의 면적과 1층의 면적은 매우 유사하므로, 이 두개의 특징의 Pearson coefficient를 확인했을 때 상관관계가 매우 높아(종속성을 가짐) 우리의 모델 H (hypothesis)가 땅의 면적에 영향을 많이 받도록 학습되는 것.
- 그렇기 때문에 feature redundant, Linearly dependent하다는 말을 하며, 시작 전 X를 invertible한지 확인해야한다.



