MoCo Review를 하기 전, MoCo에서 많이 언급되며, Contrastive Loss를 처음으로 사용한 논문으로 소개되는
Hadsell - Dimensionality Reduction by Learning an Invariant Mapping (DrLIM) in 2006 CVPR 논문에 대해서 먼저 정리하고 넘어가려고 한다. 처음부터 MoCo를 들어 갈 수 있지만, Contrastive Learning이라는 개념이 와닿지 않아 이 논문부터 시작했다. 내용도 짧고 어렵지 않아 가볍게 소개하고 넘어가겠다.
(HadSell이 구글 소속인 것과, 논문의 지도 교수님으로 얀 르쿤 교수님이 들어가 있어서 호기심이 컸던 것도 있다)
논문의 주요 Keypoint는
1. 2개의 입력 데이터를 space에 매핑하는 것이 목표이며
2. 기존에 Method는 distance metric에 영향을 많이 받으므로, 새로운 Metric을 제시한다.
3. Contrastive Loss를 제시하며, 2개의 입력 값이 이웃하면 (neighbors) 가까이 (pulled together) 2개의 입력 값이 이웃하지 않으면 (non-neighbor) 두 개를 떨어뜨려 Mapping한다. (pushed apart).
4. Contrastive Loss는 Similar한 상황, Dis-similar한 상황으로 구분되며 Euclidean Distance로 구성되어있다.
5. Contrastive Learning을 위해 따로 언급이 없지만 Self-Supervised Learning을 진행한다. (2006년 논문이라 그렇다 생각)
Contrastive Loss function
학습해야하는 파라미터 W, 파라미터 함수 G라고 할 때, X1, X2에 대한 Distance Metric은 Dw이다.

이를 통해 W에 대한 Loss function은 다음과 같이 정의되며, 최종 Loss는 아래와 같다.

def CL_Loss(x1, x2, Y, m = 1):
Euclidean_norm = torch.sqrt((x1 - x2)**2) # Euclidean Distance
return torch.mean((1-Y) * 1/2 * Euclidean_norm**2 + Y * 1/2 * torch.maximum([0], m - Euclidean_norm)**2)이 때 Contrastive Loss는 다음과 같이 정의된다.
1. Ls는 similar일 때의 Loss, Ld는 Dissimilar일 때의 Loss이다.
2. Binary CrossEntropy처럼 Label Y의 값이 0(similar), 1(dissimilar) 일 때 활성화 되는 식이 다르다.
3. 1/2은 미분의 편의를 위해, Dw의 제곱은 Euclidean Distance에서의 루트를 벗기기 위해 편의로 제공되었다.
4. Dissimilar Loss를 구하는 과정은, max(0, m - Dw) 가 들어가게 되는데, dissimilar일 경우 margin을 의미하는 m만큼 떨어지도록 학습이 되게 한다.
Algorithm
1. 각각의 입력 샘플 X에 대해 Xi와 Xj가 같은 라벨이면 Y=0, Xi와 Xj가 다른 라벨이면 Y=1이다. (self-prediction과 유사.)
2. 위에서 시작한 Labeling 작업에 대해 0일 경우 Similar Loss, 1일경우 Dissimilar Loss를 계산한다.
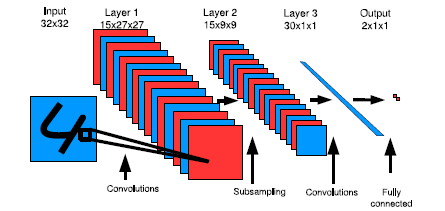
Model Architecture.
Model Architecture또한 매우 간단하다
class DrLIM(nn.Module):
def __init__(self):
super().__init__()
self.layer1 = nn.Conv2d(in_channels = 1, out_channels = 15, kernel_size = 6, padding = 0, stride = 1)
self.relu = nn.ReLU()
self.subsampling = nn.MaxPool2d(kernel_size = 3, stride = 3)
self.layer2 = nn.Conv2d(in_channels = 15, out_channels = 30, kernel_size = 9, padding = 0, stride = 1)
# self.relu = nn.ReLU(),
self.fc = nn.Linear(15, 1)
def forward(self, x):
x = self.layer1(x)
x = self.relu(x)
x = self.subsampling(x)
x = self.layer2(x)
x = x.reshape(-1, 2, 15)
x = self.relu(x)
x = self.fc(x)
return xResult
- 왼쪽이 논문 Figure 4, 오른쪽은 직접 MNIST 데이터를 통해 구현하였다.
입력 데이터의 mapping이 생각보다 잘 되지 않았으며, 학습을 오래 돌릴 경우, Mapping Space가 다 찌그러지게 된다. 따라서 왼쪽 그림을 PCA로 구현하지 않았을까 생각이 든다.
 |
 |
Appendix
논문에서 주장하는 Loss function의 유래이다. 동그란 점선이 m을 나타내는 margin이며, 중간에 지그재그로 되어있는 선이 Spring이다. 따라서 유사한 라벨은 가운데 파란 점과 최대한 유사하게 만들며, 유사하지 않은 라벨은 원 밖으로 내보내려고 한다.
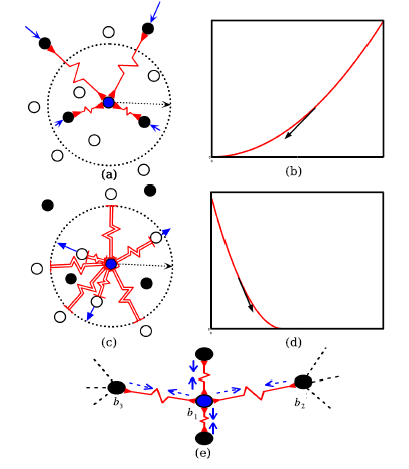

2번에서 위에서 누르는 힘을 F, 3번에서 스프링이 반발하는 힘을 K, 현재 물 수면의 위치를 X라고 할 때
F = -KX라는 공식이 나오게 된다. 스프링의 특성상 힘을 가했을 때, 원래대로 돌아오려는 성질을 가지고 있지만, 스프링이 받는 힘이 일정 범위를 넘어가게 된다면 스프링은 원래 모양으로 돌아올 수 없다. 이 이론을 활용하여 m (margin) 이라는 개념이 들어가지 않았을까 생각하게 된다. 또한 이 스프링의 모양이 복구가 가능한 상황인지 아닌지로 나누어 Loss를 만들어 냈다.
그냥 일정 범위 이상 입력 값을 떨어 뜨리기 위한 hytperparater로 m을 사용했다 하면 이해할텐데, 왜 spring analogy를 예시로 들며 설명헀는지는 와닿지가 않는다.
소스코드 및 시각화 결과는 옆의 링크에서 볼 수 있다. 소스코드 보러가기
다음은 InfoNCE Loss 혹은 MoCo에 대해 작성해봐야겠다.
논문으로 알아보는 Contrastive Learning (2) MoCo (Momentum Constrastive for Unsupervised Visual Representation Learni)
Contrastive learning의 대표적인 논문 중 하나인 MoCo에 대해서 소개하도록 하겠습니다. FaceBook, 현재 Meta인 Facebook AI research에서 Kaimming He께서 작성한 논문입니다. (ResNet 만드신 분) MoCo에 대한 개념 설
187cm.tistory.com



