피어슨 상관계수란? 두 변수 X, Y 간의 선형 상관관계를 수치로 나타낸 것이다.
수식은 아래와 같다.
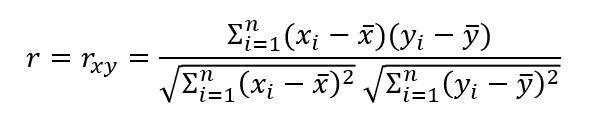
상관계수 r은 두 변수 X와 Y의 상관관계를 파악하기 위해 분모에는 각 X,Y 샘플의 표준편차를, 분자에는 공분산을 구하는 과정이 들어가 있다. 공분산 및 표준편차를 구하는 과정에서 분모의 N-1이 약분되어 위와 같은 수식을 가지게 된다.
따라서 -1 부터 1까지의 값을 가지게 되는데 아래 그림과 같은 분포가 나올 때 피어슨 상관계수 r은 그림의 글씨와 같다.

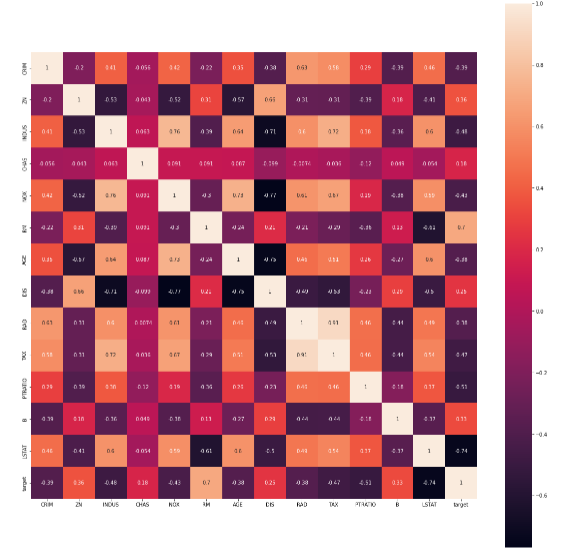
Python에서 heatmap을 그릴 때 위의 피어슨 상관계수를 활용하는데, 직접 활용하여 수치 및 데이터의 분포를 알 수 있다.
Boston Housing Value 정보를 가지고 있는 seaborn library를 활용하여 직접 실습을 진행해보았다.
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn import datasets
import matplotlib.pyplot as plt
from matplotlib import pyplot
from matplotlib import colors
np.set_printoptions(precision=6, suppress=True)
import warnings
warnings.filterwarnings('ignore')
housing = datasets.load_boston()아래와 같이 데이터를 불러 온 후, data에 데이터의 정보를, target에 데이터 별 정답을 집어넣는다.
data = housing['data']
target = housing['target']그 다음은 데이터를 Pandas 라이브러리를 통해 DataFrame형태로 만들어주고, target까지 집어넣는다.
train.head()를 통해 데이터를 잘 불러왔는지 확인한다.
잘 나온 것을 볼 수가 있다.
train = pd.DataFrame(data, columns = feature_names)
train['target'] = target
train.head()
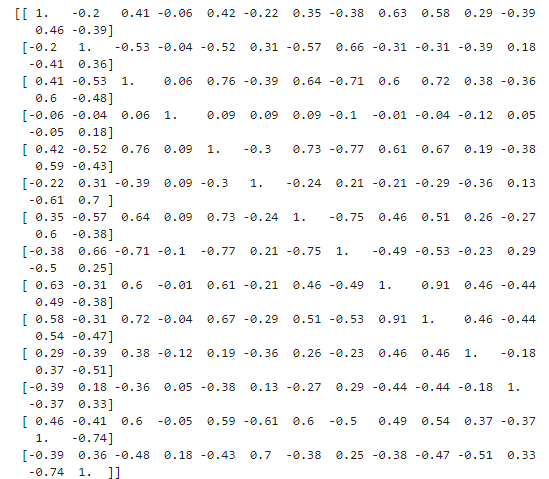
지금 이 코드가 직접 구한 상관관계 HeatMap이다.
r = np.zeros((14, 14))
for i, f1 in enumerate(train.columns):
for j, f2 in enumerate(train.columns):
deviation1 = train[f1] - train[f1].mean()
deviation2 = train[f2] - train[f2].mean()
frac_n = np.sum(deviation1 * deviation2) #numerator
frac_d = np.sqrt(np.sum(deviation1**2)) * np.sqrt(np.sum(deviation2**2)) # denominator
r[i][j] = round(frac_n/frac_d, 2)
print(r)아래는 직접 구한 후, print()로 시각화 하였을 때의 그림이다. 하지만.. 예쁘지가 않다... sns.heatmap() 을 통한 내장함수와 비교하면 좀 많이.. 예쁘지가 않다..ㅜ 그래도 수치는 자세히보면 똑같은 것을 볼 수 있다.
하지만, 적절한 코딩을 추가해주면 근사한 Heatmap을 만들 수가 있다.
내장함수를 사용하는 것도 좋지만, 어떻게 만들어지고, 어떻게 저런 수치가 나오는지 직접 해보는 것도 좋은 것 같다.
마찬가지로 분포도 그릴 수 있다. 하지만 두개로 나누어서 보면 번거로우니까 둘로 합쳐보자
# # HeatMap그리기
# 그림 크기 조정
plt.figure(figsize=(10,10))
# x 및 y 축에 레이블 추가
plt.xlabel("x axis", size = 14)
plt.ylabel("y axis", size= 14)
# 플롯 제목 추가
plt.title("Pearson Correlation Coefficient", size=28)
# x 및 y 축 모두에서 눈금 조정
plt.xticks(ticks = np.arange(0,14), labels = train.columns)
plt.yticks(ticks = np.arange(0,14), labels = train.columns)
for i in range(14):
for j in range(14):
plt.text(j, i, '%.2f%%' % (r[i][j] * 100), ha='center', va='center', color='red', fontsize=8)
# ".imshow"메소드를 콜링 할 때 색상 맵 할당
plt.imshow(r, cmap='GnBu')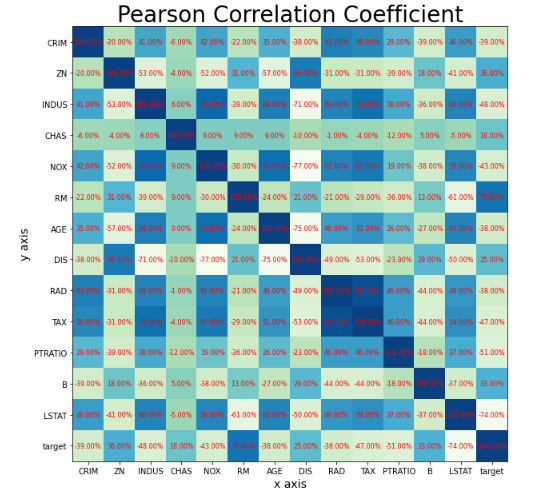
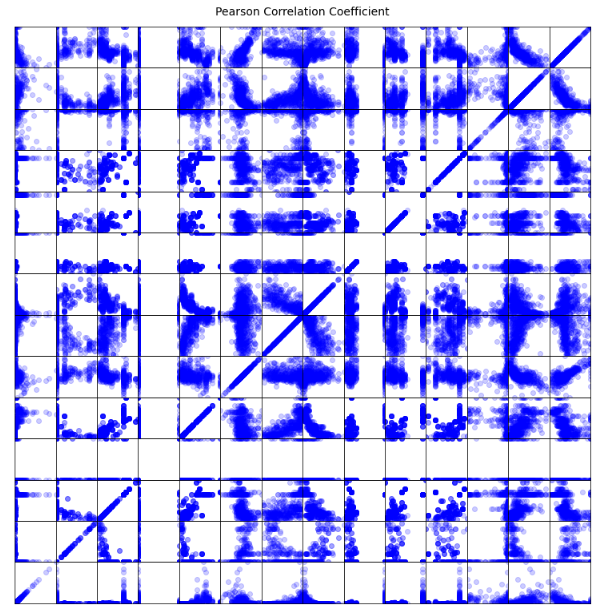
# 분포 그리기
fig = plt.figure(figsize=(10, 10))
for i in range(14):
for j in range(14):
# 분포를 틀로 표시
ax = plt.axes([i / 14, j / 14, 1 / 14, 1 / 14], aspect='auto')
ax.scatter(train[train.columns[i]], train[train.columns[j]], color='blue', alpha=0.2)
# 틀 경계에 격자 그리기
ax.xaxis.set_ticks_position('none')
ax.yaxis.set_ticks_position('none')
ax.spines['top'].set_visible(True)
ax.spines['right'].set_visible(True)
ax.spines['bottom'].set_visible(True)
ax.spines['left'].set_visible(True)
ax.grid(color='gray', linestyle=':', linewidth=0.5)
# 축 범위 설정
ax.set_xlim(train[train.columns[i]].min(), train[train.columns[i]].max())
ax.set_ylim(train[train.columns[j]].min(), train[train.columns[j]].max())
# 축 눈금 조정
ax.set_xticks([])
ax.set_yticks([])
# 그림 제목 설정
plt.figtext(0.5, 1.02, "Pearson Correlation Coefficient", ha='center', size=14)
plt.subplots_adjust(wspace=0, hspace=0)
plt.tight_layout()
plt.show()둘의 소스코드를 종합하면 다음과 같다
분포와 HeatMap을 동시에 볼 수 있다. 하지만.. 이상하게 오류가 발생한다.. 그림에 숫자만 넣으면 완벽한데 이거 때문에 며칠을 날렸다. 그래서 어쩔 수 없이 분포에 숫자를 넣었다. 소스코드는 아래와 같다.
HeatMap과 분포도 같이보기. 자그마난 프로젝트 끝.
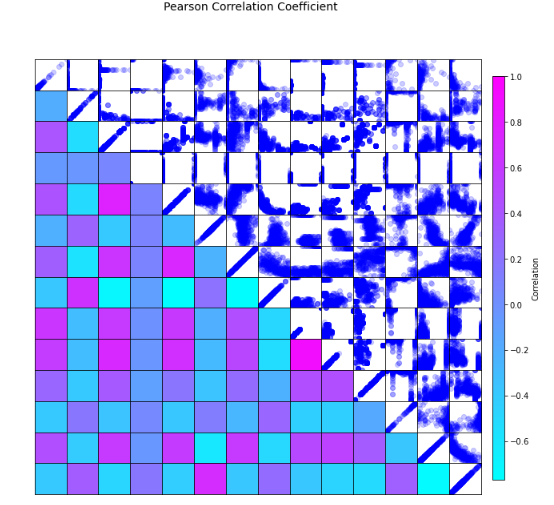
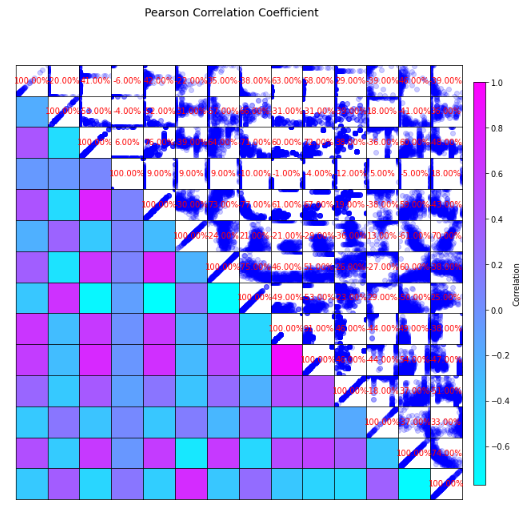
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
# 데이터 생성
target = housing['target']
data = housing['data']
train = pd.DataFrame(data, columns=feature_names)
train['target'] = target
r = np.zeros((14, 14))
for i, f1 in enumerate(train.columns):
for j, f2 in enumerate(train.columns):
deviation1 = train[f1] - train[f1].mean()
deviation2 = train[f2] - train[f2].mean()
frac_n = np.sum(deviation1 * deviation2) # numerator
frac_d = np.sqrt(np.sum(deviation1 ** 2)) * np.sqrt(np.sum(deviation2 ** 2)) # denominator
r[i][j] = round(frac_n / frac_d, 2)
fig = plt.figure(figsize=(10, 10))
# 그래프 영역을 그리드로 설정
grid_spec = plt.GridSpec(14, 14, wspace=0, hspace=0)
# 좌측 플롯
for i in range(14):
for j in range(14):
if j >= i:
# 분포를 틀로 표시
ax = fig.add_subplot(grid_spec[i, j], aspect='auto')
ax.scatter(train[train.columns[i]], train[train.columns[j]], color='blue', alpha=0.2)
# 틀 경계에 격자 그리기
ax.xaxis.set_ticks_position('none')
ax.yaxis.set_ticks_position('none')
ax.spines['top'].set_visible(True)
ax.spines['right'].set_visible(True)
ax.spines['bottom'].set_visible(True)
ax.spines['left'].set_visible(True)
ax.grid(color='gray', linestyle=':', linewidth=0.5)
# 축 범위 설정
ax.set_xlim(train[train.columns[i]].min(), train[train.columns[i]].max())
ax.set_ylim(train[train.columns[j]].min(), train[train.columns[j]].max())
else:
ax = fig.add_subplot(grid_spec[i, j], aspect='auto')
normalized_value = (r[i][j] - np.min(r)) / (np.max(r) - np.min(r))
color = mcolors.rgb2hex(plt.cm.cool(normalized_value))
ax.patch.set_facecolor(color)
# text_x = (train[train.columns[i]].max() + train[train.columns[i]].min()) / 2
# text_y = (train[train.columns[j]].max() + train[train.columns[j]].min()) / 2
# ax.text(text_x, text_y, '%.2f%%' % (r[i, j] * 100), ha='center', va='center', color='red', fontsize=10)
# 축 눈금 조정
ax.set_xticks([])
ax.set_yticks([])
# 우측 색상 막대
cmap = plt.cm.cool
norm = mcolors.Normalize(vmin=np.min(r), vmax=np.max(r))
sm = plt.cm.ScalarMappable(cmap=cmap, norm=norm)
sm.set_array([])
cb_ax = fig.add_axes([0.92, 0.15, 0.02, 0.7])
cb = fig.colorbar(sm, cax=cb_ax)
cb.set_label('Correlation')
# 그림 제목 설정
fig.suptitle("Pearson Correlation Coefficient", size=14)
# 이미지 저장
plt.savefig('correlation_plot.png')
plt.show()
'Machine Learning > Statistics' 카테고리의 다른 글
| AI 학습데이터가 진짜 고갈될까? [논문리뷰] - Will we run out of data? An analysis of the limits of scaling datasets in Machine Learning. (2) | 2024.04.05 |
|---|---|
| Self-Attention과 Bilinear function (2) | 2023.10.02 |
| Variational Bayes Tutorial (0) | 2023.06.08 |
| Sigmoid 미분하기 (0) | 2022.09.20 |


