The relative entropy is a measure of the distance between two distributions. -> D(p||q)
D(p||q)= a measure of the inefficiency of assuming that the distribution is q when the true distribution is p라는 의미이다.
참인 분포 p에 대해 비교를 원하는 분포 q와의 비효율성을 확인하는 단계이다.
Ex
만약 우리가 p 분포를 알면, 평균 길이가 H(p) bit인 코드를 설계 가능, 하지만, 우리가 분포 q에 대한 코드를 쓴다면?
H(q) + D(p||q) 가 되어야 한다.

- 그래서 이를 구하는 수식은 다음 2.26과 같이 정의하고, KL divergence loss 혹은 Kullback-Leibler loss라고 부른다.
- 앞서 설명에서 비효율성이라 설명을 하였기에, 둘의 분포가 같은경우 D(p||q)의 최솟값은 0이 되며 가장 큰 값은 무한대까지 발산하게 된다.

However, it is not a true distance between distributions since it is not symmetric and does not satisfy the triangle inequality. Nonetheless, it is often useful to think of relative entropy as a “distance” between distributions.
-> 위의 설명처럼, 두 분포 사이의 거리 정도로 생각하면 될 것 같다.
그래서 이 거리 말고, 이 둘 사이의 정보량을 확인하고 싶기에 나온 것이 바로 Mutual information 이다.
=> 하나의 Random Variable이 다른 Random variable을 얼마나 포함하고 있는지이다.

- 수식으로 나타내면 위와 같으며, I(X,Y)이다. 이 값은 KL loss를 응용하여 이루어지는데, p(x,y)와 p(x)p(y)의 거리 차이를 나타낸다고 생각하면 된다.
- 둘의 상호작용으로 p(x,y)의 값이 증가한다면 정보량 또한 많아질 것이며, 둘이 독립으로 관계가 없다면 log 1 = 0이 되어 정보량의 공유가 없다고 생각할 수 있다.

- 또한 I(X;Y) = H(X) - H(X|Y) 로 생각할 수 있다. 이 뜻은 X에 대한 불확실한 정도를 Y를 통해 얻을 수 있는 정보로 줄이겠다는 뜻이 된다.


- 그리고 위에서 유도한 첫번째 수식을 바탕으로, 두번째 수식을 정리하면, 마지막과 같은 그림이 나오는데, 이는 우측의 그림에서 I(X;Y)가 밴 다이어그램에서 교집합 부분에 해당한다는 것을 알 수 있게 해준다.
- 아울러, 앞서서 우리가 본 모든 수식이 교집합 부분에 해당한다는 것을 알 수 있다. (참고:위키피디아 Conditional entropy)

- 그래서 자기 자신에 대한 Mutual information은 H(X)이다.
2.5 CHAIN RULES FOR ENTROPY, RELATIVE ENTROPY, AND MUTUAL INFORMATION
- 이번 강좌는 특별할건 없고, Chain rule을 통해서 여러개의 Random variable을 다루는 것으로 시작을 한다.


- 가장 먼저 첫번째 Theorem, chain rule for entropy라는 정의인데, Baysian rule을 여러개로 펼친다고 생각하면 될 것 같다.
- 그리고 우측에 존재하는 Proof는 다른 방식의 Proof인데, Π의 파이 기호는 덧셈을 축약한 Sigma 기호를 곱셈 버전으로 만들었다고 생각하면 될 것 같다. 그리고 이 Π 곱셈 기호는 Log와 만나 Sigma로 바뀌고, 똑같이 유도됨을 볼 수 있다.

- 그리고 이 부분은 Conditioanl Mutual information의 수식이다.
- 위의 수식의 증명은 아래와 같이 해결할 수 있다.

- Mutual information 또한 Chain rule성질을 만족한다.

- 아래와 같이 KL divergenece loss인 relative entropy 또한 chain rule 성질 만족.
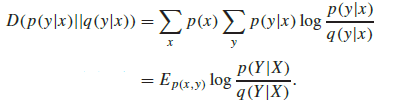
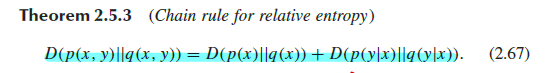
- 조금 더 구체적인 수식 전개.
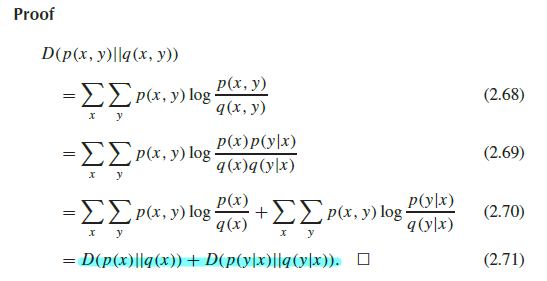
'Information Theory' 카테고리의 다른 글
| 7-4 PREVIEW OF THE CHANNEL CODING THEOREM (2) | 2023.12.03 |
|---|---|
| 7.2 7.3 SYMMETRIC CHANNELS, PROPERTIES OF CHANNEL CAPACITY (1) | 2023.12.01 |
| 7-1. CHANNEL CAPACITY (2) | 2023.11.30 |
| 2.6 JENSEN’S INEQUALITY, Convex function. (2) | 2023.11.19 |
| Chapter 2-1, 2-2, ENTROPY | Information Theory. (0) | 2023.11.18 |



