링크 : https://proceedings.neurips.cc/paper/1993/file/9e3cfc48eccf81a0d57663e129aef3cb-Paper.pdf
제프리 힌튼이 1993년 NIPS에 투고한 Autoencoder에 대한 내용을 가볍게 알아보자.
분명 Masked autoencoders are scalable vision learners에 대한 논문을 읽고 있었는데, 갑자기 참고 문헌을 보다가 새버렸고, 빠져들었다.. 너무 깊게는 말고 간단하게 다뤄보자.
Masked Autoencoders are scalable vision learners를 읽다가 PCA, k-means가 Autoencoder라는 내용을 보고, 음..? 하는 생각에 참고 문헌까지 들어왔다가 너무 깊게 빠져버렸다. 어쨌든
- Masked Autoencoders are scalable vision learners주장 : PCA, k-means가 Autoencoder이다.
- 이 논문의 주장은 MDL (minimum description length) 를 통해 Autoencoder를 효율적으로 학습하는 것을 보인다.
- PCA는 weak autoencoder이다.
논문을 들어가기 전,
Encoder: set of recognition weights
input vector: 입력 값
code vector: latent space
Decoder: set of generative weights.
이 논문은 Sender와 Receiver가 Vector를 주고 받으면서, 그 안의 bit의 수를 알아 맞추는 게임이다. 즉 통신에서 Sender는 training vector의 앙상블을 압축해서 Receiver에게 보내야 하며, Receiver는 다시 원래대로 복구를 해야한다.
그림으로 그리면 이런 그림이려나.. 못그려도 이해좀.. 부탁한다.. 통신, 멀티미디어에서 부호화랑 복호화를 생각하면 된다.

이렇게 sender와 Receiver가 서로 통신을 할 때, sender는 모든 입력 vector를 관찰 후, Receiver에게 전달하면 된다. 따라서 굳이 online method를 할 필요는 없다. 정보 수집해서 보낸다고 할 때, i번째 요소의 c번째 vector를 x_i,c로 정의하자.
우리의 그림은 요소가 1개인 상황이다. Sender와 Receiver가 확률 분포에 대해 동의를 했다면, value x에 대한 확률 p(x)를 정의할 수 있다.
x가 평균 0 분산이 σ^2 인 가우시안 분포를 가지고 있다면, Shannon's coding theorem에 의해 communicated cost는
- log p(x) bit으로 정의할 수 있다. 여기에 quantization width를 t라고 정의한다면 우리의 communication cost는
- log t + 0.5 * log (2πσ^2) + x^2 / 2σ^2가 된다.
하지만 위의 수식은 wastful 하다고 Hinton선생님께서 말하신다. 그 이유는 vector의 요소 앞서 정의한 (i)가 관계가 있을 때, 더 효율적으로 input vector를 communication 전에 바꿀 수 있다는 것이다.
그것이 바로 MDL이 되겠다. MDL이란 minimum description length principle으로, 데이터의 최적의 모델은 total number bits을 하나로 minimize 한 것이라는 이론이다. 모델을 학습 하거나 예측하는 것은 데이터에 대한 규칙성을 포착하는 것 이므로, 더 많은 데이터를 압축할수록 우리는 더 많이 정보를 알 수 있다는 이론이다.
Autoencoder는 편리하게 total description length를 3개로 쪼갤 수 있다고 하는데, 아래 그림과 같다.
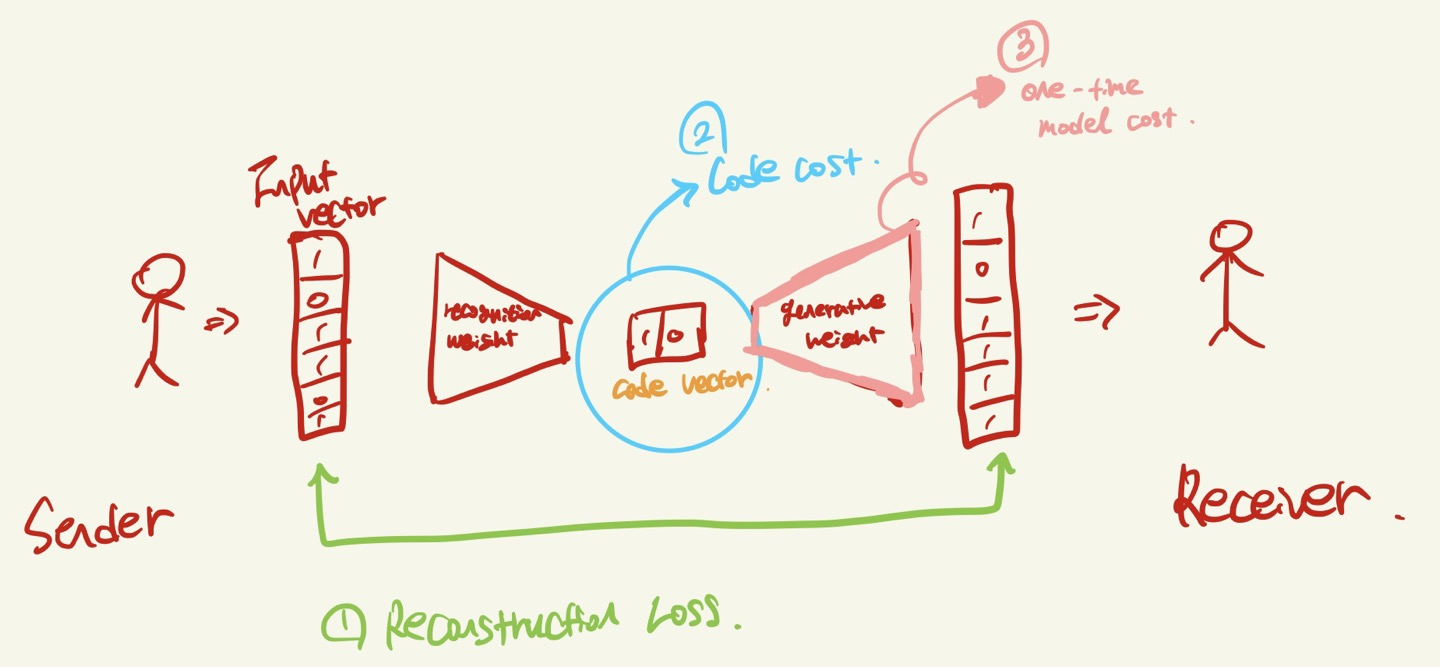
1. Reconstruction Loss? Cost,
2. code cost
3. one-time model cost → 하지만 이번 논문에서는 무시.
그리고 위에서 크게 언급하진 않았지만, 논문에서 언급한 내용은 PCA든 VQ든 code cost는 무시한다. 즉 reconstruction cost만 활용하겠다 라는 것이고, 이유는 우리가 위에서 zero mean과 same distribution Gaussian으로 가정했기 때문이다


하지만 우리는 PCA나, VQ를 하는게 아니므로 다시 돌아와서 code에 대한 energy E를 정의한다 (왼). 우리의 energy는 input vector의 차원인 k, prior probbility π, reconstruction error d^2이다. 이 에너지는 나중에 볼트만 분포를 따라 특정 코드를 결정하는게 이용된다.
Energy는 code cost의 합 + reconstruction loss 이다. 따라서 input vector의 차원인 k에 대해 모두 더하기에 k가 붙었으며, 기존의 수식에 prior π에 대해 entropy가 붙은 것을 볼 수 있다.
오른쪽의 < ... > 는 Expectation을 나타낸다. 즉 cost에 대한 기댓값은 E에다가 정리를 해두었으므로 E에 대해 정의된다.



우리는 online training이 아니므로, 모든 벡터에 대한 요소를 보고 학습을 진행한다. 따라서 어떤 분포로 communication이 될지 알 수 있다. 앞서서 정의한 shannon's coding theorem과 가우시안 분포를 통해 랜덤 비트에 대한 기댓값 H는 제일 왼쪽의 수식처럼 정의할 수 있다.
F는 헬름홀츠 free energy로, 위에서 정의한 Energy의 기댓값에 랜덤 비트의 기댓값 H를 빼준 값이다.이 친구를 통해 우리의 latent space 분포대로 잘 만들어지도록 한다.
pi는 posterior distribution을 의미하며, Softmax와 유사한 꼴이 되었다.
목적함수는 squared reconstruction loss를 사용하였으므로 따로 다루지 않겠다.
아래 그림은 결과 이다.
